Why my work is sort of bad but I shouldn't feel (too) bad about it

I'm writing this for two purposes. One, to cover criticisms I already know about my work from anyone who might read it, though not even my mom reads my work so I'm not sure from what dimension these hypothetical criticisms would come. Two, to describe my autodidactic journey toward a basic education in statistics, which may be of interest to others who've done the same.

A series of steps by which you could get the answer if you didn't understand what you were trying to do.

During college, I appreciated the value of statistics not through courses—obviously, because who could find STATS 101 interesting?—but in baseball. Baseball's always been my jam, as it's what I think of as the introvert's sport. The game's actions merely mimic teamwork; everything on the field occurs not between humans but between one human and a mundane object called the baseball, thrown and hit by humans but, when encountered, entirely divorced from them.

It's the coolest sport.

I followed the great contemporary sabermetricians Tom Tango, Patriot, Phil Birnbaum, and many others. I learned that batting average was a poor statistic not because it couldn't show what it had intended (it showed exactly what it had intended), but because people used it to answer the wrong questions. "Who's the best hitter," for example, is better answered by a statistic like weighted on-base average (wOBA), unless you literally mean hitting the baseball with the bat most often—which is a weird question to ask.

I naturally did what any convert would; I joined several baseball forums to explain why everyone was wrong. I remember sitting in a parking lot with The Book memorizing equations as if cramming for an exam. After all, I had to inform a lot of people online that they were wrong about baseball, so I had to know the material cold.

I only noticed classical statistics when some academic researchers started muscling in on the sabermetricians' territory. I vaguely remember arguments between the camps, although academics like Cyril Morong already had some cred as sabermetricians. The tension between these worlds was high enough for Tom Tango to sarcastically bemoan his rank as "just some schmoe" who wasn't "highly educated enough" (Sidenote: Tango remarks that academics who "shun logic in favor of regression" should "watch a game," a kind-of-ironic comment given that "watching a game" was the de facto traditionalist rejoinder to the kinds of counterintuitive insights his own work had uncovered).

These academics championed regression, and I suddenly felt lost in a world that had once felt so familiar. My comforting acronyms (wOBA, OPS, WAR) were replaced by alien ones (OLS, GLM, R^2, RMSE), and, worse, these acronyms brought not commonsensical explanations but copious math baggage. On-base plus slugging (OPS) was straightforward: you added on-base percentage and slugging percentage, just as the name said. Ordinary least squares, on the other hand, had all sorts of strange symbols like Big Sigma and related to these things called residuals.

I'm not writing a casual history of sabermetrics, so I'll parse a ton of debate and conclude that the sabermetricians seem to have won the day. Today most baseball analysis uses my preferred acronyms. I don't recall if an academic found this, or if it was merely proof of concept from a sabermetrician, but regression formulas kept misrepresenting the value of a triple. Indeed, if you just regressed runs scored on triples, you'd find that triples had negative value, i.e. as you hit triples you should expect your runs to decrease.

To quote Bizarro Morpheus Diddy,

Hold up.

As Phil Birnbaum explained, this was probably due to the types of teams that hit triples. The model didn't know that triples were predominantly hit by faster, weaker hitting teams. Powerful teams had homerun hitters, and those guys often crossed third base not at breakneck speed but a trot. So, hitting lots of triples appeared to make you score fewer runs relative to the other outcomes.

Or, as Richard McElreath wrote some years later: regression is a cruel oracle.

And with that, I dismissed the academics and their regressions.

Academic statistics

Let's fast forward to when I joined a project with my program's first-year writing director. We were interested in the effect of an embedded librarianship intervention. Given my hobbyist background, in which I knew my means from medians from modes—maybe—I took charge of the project's statistics. When it came to the stuff of sabermetricians I was competent; I could describe data, tidy up a spreadsheet, and even write code to automate tasks such as scoring the participants' pre and post-test exams.

But academics weren't like sabermetricians. They cared about things like p values and R^2. They didn't really explain much; they'd write, here's the model we built, and here are some citations saying why it's appropriate, and we did such and such a correction because of this citation, and we acknowledge that some assumption is not really met, but our model, with the aforementioned correction, is robust to that violation—and so on.

You had to speak in terms of null hypotheses, and you couldn't say those were proven right or wrong. You could say that you failed to reject the null, and a 95% confidence interval, which seemed like it should be the percentage chance to contain a true value, didn't mean that at all.

It was all very confusing.

And although I came to learn much later that many researchers had abandoned p values altogether, it didn't make any impression on my world. Indeed, I have learned that many academic problems, once identified in the literature, are promptly ignored. An example I know well is the library one-shot session, which is when a librarian visits a class once a semester (the one-shot) to discuss something related to the library's purpose. It's pretty much a waste of time. I found reference in the literature to 1988 where one shots were "universally lamented by university librarians." Yet over 30 years later basically every academic library still uses one shots or some marginal improvement over them.

Anyway, my mass confusion meant that I had to dig into the world of traditional academic statistics. I got some mentoring and textbooks, pouring over linear regressions. It was dull, and I took a lot of it on faith, but after long and careful study I learned that the goal of research was simple: find p < 0.05. Sure, lots of people said not to do that, but it seemed like every journal I consulted cared loads about p values. They didn't always have to be < 0.05. Since alpha is arbitrary, we could set it 0.1, and we could even say our finding was "marginally significant" or maybe "approaching traditional significance." The point was, you hunted p values.

Truth.

What's more, and especially neat for someone whose piss poor math education deserves its own post, you didn't need to know any math to build these models. I used this amazing program called SPSS where you just clicked buttons and the ghost in the machine did everything.

For our project, the statistics were very simple, because there was no difference at all between the experimental and control groups. You didn't need inferential tests because the (lack of) effect was obvious. On virtually all of our assessment measures, the control and experimental groups showed similar improvements, which is to be expected from a maturation effect.

Sidenote: something I've learned since then is to just report whole numbers 99% of the time. On 100-point exams with standard deviations around 20, there's no difference between 55% and 55.12%. To be fair, I had read in a book that you're supposed to use 2 decimal points. That was honestly in a section of a book discussing how to report statistics (here it is in random lecture notes). I guess it's like the passive voice: an artificial, superficial, and deeply needless way to assert objectivity.

The paper's main analysis was an ANOVA comparing two groups. That's pretty weird. Mathematically, an ANOVA between two groups is the same as a t test; the F statistic is just t squared. So why didn't I use a t test? I was learning all of these different methods and wasn't sure which to choose. That's the thing with academic research; it's quite confusing to newcomers. The sabermetricians valued clarity: here's what I want to do, say predict a pitcher's performance, and here's how I tried to do it, say by isolating these variables over which the pitcher has control and ignoring the noise.

Academic statistics are like, here's this impressive sounding method, replete with equations, dropped right in the middle of the paper in case you had any doubt that I'm an expert. I think that every paper I've read which uses multilevel modeling painstakingly explains what a multilevel model is, including equations, as if there aren't a billion references in the world about them. It's like the statistical equivalent of the literature review, an insufferable practice in which each and every paper published is supposed to recast the history of its chosen topic, aka, operate as part of a massive citation generating machine, further confining us to the dread dimension of impact factors and citation metrics.

Pretty standard, super approachable table

So at the time I was kind of confused about what method to use; I had juggled between the "gain score" of a t-test and a repeated measures ANOVA. They seemed to do the same thing, but elsewhere in the paper I had used a repeated measures ANOVA, and I had to do that because I didn't want to commit a familywise error, which sounded really bad. I went with the ANOVA for the main comparison so I wasn't explaining two methods, the t test and the repeated measures ANOVA.

Like, who the eff even knows.

Fortunately, the project's design was solid. My co-author had studied research design and her father, our impromptu consultant, had considerable industry experience. We accounted for, like, everything, randomly assigning teachers, librarians, and students to control and intervention groups, using a new and standardized curriculum, designing assessment measures (based on the literature) that didn't reward "teaching to the test," and issuing those assessment measures many weeks apart to nullify short-term gains.

I'm also glad to put a negative finding out there. We tried this thing that you might be considering, and you might not know this but we were super invested in finding a positive result (we were funded by a campus seed grant, after all), and, well, we got nothing. Maybe it could work, given the right circumstances, but the method itself isn't magic, so don't expect magic.

While I was totally unaware of the replication crisis, this project taught me to be skeptical of published results, right out of the gate. Here we were, in good faith trying an intervention that had success in the literature and much testimony about its utility—and to say the least it did not replicate.

If I had to speculate why, I'd propose that we were fooled by publication bias resulting from questionable research practices, i.e., a preponderance of positive findings generated by low-powered studies with trivial assessment measures and poor research design. Like, one study issued pre- and post-tests to students in a random class against one in a class designed to cover the material on the post-test. In another study, the treatment group had its grades tied to the pre- and post-tests whereas the other groups received gift certificates. I'm not joking; that happened (p. 375).

If I can't download your data, get outta heah

I'm not sure why I didn't push for open data early on, because sabermetricians sure valued it. In fact, when discussing the peer review model as a writing instructor, I'd often contrast it with what I had seen sabermetricians do. Peer review's a closed model where anonymous gatekeepers decide which work's worthy of dissemination, and if they do, then it becomes so much like gospel. In contrast, sabermetricians would post their work on blogs and solicit candid input.

But, anyway, I didn't. I thought it important to shred our data because the IRB said we would after some period of time, and that seemed responsible. After all, we used the data for our research projects, and those projects were finished. The journals published our work without further question. Who would need the data?

On this next project, I had read over 100 student essays to evaluate synthesis claims. And the results surprised me, despite having taught in the program for many years. I found that students didn't bother synthesizing outside material at all, unlike how they had approached their class readings. When instructors emphasized materials, students wrote about them. This seemed obvious in retrospect, but I wondered how many instructors just asked students to "find a source," which the students inevitably tacked on. I knew I did that as well as some of my colleagues. And now it looked like a lot of our program's teachers were also doing it. What if everyone was doing it?

Yet there's no data for you to review, so you're taking my word for it. At the time, this seemed reasonable. First of all, we said we'd destroy the data in our IRB, so destroy the data we did. Second, I'm the freakin' author, and freakin' authors speak Truth. The peer reviewers screened the paper. And if you have any questions about how I scored the essays, I included a sample of what I had considered a 0, 1, 2, and 3, as well as my rubric.

Obviously, I'm not claiming that I lied or falsified data. I'm not even saying I had an unconscious desire to reach a preconceived conclusion; I remember rereading these essays several times so that I was confident and consistent in my scoring (I was working a desk job at the time, so what else was I going to do?). I'm saying that you're basically trusting one guy's read of 100 some odd essays at one university to make judgments on your program. Wouldn't you like to compare notes at least? Wouldn't you like to read maybe 10 of the papers and see if they're like the papers at your school and if you're more or less in agreement with me?

The statistics are a little better here, in that I clarify what things mean, but that's because the journal asked me to do so. I also did a post-hoc test, so I had to read all about those and which to choose. It had a purpose, too, because the ANOVA, an omnibus test (look how much I learned!!!), couldn't tell where the differences were significant. Of course, because I compared three groups I could've told you where they were just by looking at them...but that doesn't look very intimidating. Better to use Tukey's HSD and quote Q statistics.

I also want to say that the peer review process really helped here. I want to write about my bad experiences with peer reviewers, because that's fun, but this is one of those times where I submitted a draft which, upon reflection, was pretty poor, and the reviewers trusted in its potential.

Open data shouldn't be scary. I think some authors may worry that academic hitmen, you know, methodological terrorists, are buried in spreadsheets at all hours, gunning to embarrass everyone. And in the case of errors that affect results—well, sure, you should duck and cover. We learned in the COVID-19 pandemic that shoddy work carries real-world consequences, and that shoddy work has to be called out, and we should get in the habit of calling out shoddy work so that when the stakes are high we're ready for, and receptive to, uncomfortable criticisms. There's some anarchist argument like that, which says we should get used to breaking rules so that when we have to break some really big rules, we're OK doing it.

But in some cases, especially for textual data, open data can help reveal and contextualize differences of opinion, as is the case for writing assessment. Say you read three of my students' essays and would've scored them 3, 3, 2 on a 3-point scale and I had scored them 2, 2, 1. That doesn't mean one of us is necessarily wrong. You should just know that there may be what you consider a meaningful bias, as I deflated scores more than you would have. That doesn't mean we retract the paper. That doesn't mean the paper's "invalid." It means you have more information available to decide how well this research applies to your particular circumstances.

Isn't that good?

"Nowadays, maybe not so much like fifty years ago, but nowadays, if there's a single authored paper with data, that's a red flag right away." -Roger Peng

Rate My Attitude. I have a bigger love/hate relationship with this paper than I do with Breaking Bad's Season 5, and that's saying something considering I vacillate between binge watching Season 5 YouTube clips vs. frantically Googling phrases like "breaking bad season 5 worst ever."

Where do I even start? Ok, something minor. After the paper was published, I noticed the language was wrong. It said that events were x more likely to happen when it should've said odds. I was surprised I missed this, because I used to be a poker player. It's why I think the convention that power = 80% = acceptable is totally bonkers. Those are the same odds, 4-1, that aces beat kings in poker. And I lost aces to kings many times (I'm sure it was more than 20%, as any poker player would tell you, but my database is long gone so you'll have to take my word for it). No way do I want to put in a ton of work designing and executing a research study only to take what is to any poker player a run-of-the-mill badbeat.

This is your grant on 80% power.

Anyway, I asked the journal to correct that, but it wouldn't. This is a problem with traditional publishing, if you ask me. They don't like to change anything because they're affecting the "written record." Come on y'all. It's not 1834 anymore. You're not the Royal Society. Just update the paper with a note that says, the author noticed language errors in the following places and we corrected them. Done and dusted. But nope. I get a response from a supporting editor that it's not possible and (paraphrased) that I should move on with my life.

The biggest problem, though, is that I did a logistic regression. I had just completed Gelman and Hill's book on multilevel modeling, so I had originally built a hierarchical model, nesting RateMyProfessor scores within instructors. Yet I was also receiving some mentoring from a prolific researcher in biomedicine who had recommended I do a logistic regression...and I admit that I liked the rhetoric of it. It sounded really cool to say the odds of this were x times greater than y. Definitely better than, here's some lame slope like every other lame slope.

Obviously this is bad, for at least one big reason: we lose a lot of information. We take perfectly nice continuous data and dichotomize it. Discarding information should be an absolute last resort; you shouldn't voluntarily do it.

Then the actual regression is weak. A reviewer asked that I account for various biasing factors that had been shown to influence SET results. I didn't really agree with this, because these biasing factors are unbelievably overblown, so I kind of halfheartedly threw them all in a model and wrote something up at deadline, so it didn't even name the reference value.

I should've just reported my hierarchical model, which would have appropriately handled the nested data rather than the method I had used, which was to average scores for instructors. Then all of the issues I had with logistic regression would have disappeared, because I wouldn't have used an incorrect method of analysis. It's a testimony to stupid human stubbornness; I had finished a book on multilevel modeling, which taught me how to handle nested data, but rather than use what I had literally just learned from two superheroes I sought to justify an inferior method solely because I had attached it to a submission.

Putting the questionable modeling aside, I think the paper covers a vital topic. Motivated reasoning is a big problem in academic research, as much as we might want to pretend it isn't. And it's a massive problem in SET research, and not for the reasons often articulated, i.e., unscrupulous vendors want to shill SET products to unsuspecting university administrators. Faculty are just as financially compromised as SET companies. As they often bemoan, their tenure and promotion standards, and even whether they're fired or hired, rely in part on SETs. Discrediting SETs certainly serves their financial motives.

As part of another project, I was reading SET literature and couldn't help but notice the endless complaining. It got to the point where I asked, "Why are so many people whining so much?" More than a few of these people were credible researchers in their own fields, so I began to wonder whether they had a grudge against SETs because their own scores were bad. I went about reading a bunch of their work and classifying them as (1) "deniers," (2) "neutral," (3) or "apologists," and the effect was absolutely massive. I wasn't totally surprised that the deniers were so low; it helped explain why they spent so much time bashing SETs. I was surprised that the apologists were so high; here were people who wrote maybe one or two papers on SETs, that's it, and overall they did really well on RMP. But then, it's not much of a mystery, because I did well on my SETs (and my RMP) and here I am defending them as valid instruments.

Many of the researchers were easy to classify, like Dennis Clayson and Philip Stark, who have built virtual media empires around SETs, and Bob Uttl who actually believes SETs violate human rights (slide 36). But many others were not and required some nuanced readings, and I may have gotten some of them wrong. I think I read each essay, all told, at least three times. I read through the sample first without peeking at RMP scores, to help unbias my results, but the other times I read them knowing what the original results were. If you want the dataset to see how I classified researchers, here it is, and here are the results of a basic HLM.

m <- lme(score~attitude,random=~1|name,data=rmp)

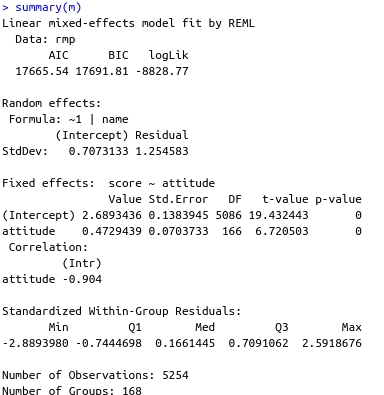
I think the neutral group obscures the difference of (IMO) interest between the deniers and apologists. Ugly graph inc, which shows how, as the attitude "improves," the scores also improve. PS: the median denier score is 3, which is pretty bad; the average RMP score, when I had crawled the site, was 3.7. I thought it was funny how the neutral group averaged the actual average.

Anyway, hence my love/hate relationship.

Seriously guy: Don't put a method in your title

Clearly the problem in this paper is putting "regression analysis" in the title, as if that's novel. Takeaway: only put a method in the title if the method itself is relevant. Here, it isn't. In my defense, library science isn't the most statistically rigorous discipline. You don't find many regression models. I wanted to identify my work as regression, in other words, to signal that it was a serious piece of writing based on serious methods.

At this time, I'm learning fairly basic stuff and moving away from R^2, for lots of good reasons, but I'm stuck on the p value. It actually has its own column in this paper. It's also the paper where I finally stopped using SPSS in favor of R. You can see a relic of SPSS in this paper, in that I label error as the Standard Error of the Estimate, which is what SPSS calls the RMSE—which is what R calls the Standard Error of the Residuals (I don't know anymore). This paper took me so long to write that by its end I had transitioned fully to R but preserved notation from an early draft done in SPSS.

I would put a screenshot of SPSS here but I can't imagine reinstalling it on any partition I own and I don't want to jack someone's image and get DMCA'd for making fun of SPSS.

Anyway, that Standard Error showed that I was now moving beyond simple correlation values. Could we predict anything? Was the model actually useful? I wouldn't explore this in more depth until tackling machine learning, but it was a start.

Now, suppose you tasked someone who had a totally improvised and informal statistics education to perform causal analysis. You tell this person, "You understand that correlation does not equal causation, and you also understand, through reading random Reddit posts and blogs, that nevertheless you can perform causal inference in regression, and that you should cite some mathmagician named Judea Pearl."

This person might use partial correlations? And he wouldn't cite Judea Pearl.

I wanted to answer the question: which socioeconomic factors, all of which confound one another, contribute most to library funding? I thought partial correlations could answer it, like, if one variable retains its correlation after partialing, then it was the dominant one. And because education always retained its high r values, I concluded that education above all mattered. It's a point sharply made in Table 3, where the r of 0.85 absolutely dwarfs everything else.

But I made a mistake. I had calculated a statistic called "educated residents," which was simply the community's estimated population * its estimated percentage of adults 25 or older with a Bachelor's degree. Population overwhelmingly correlated with a library's income, far more than anything else, but I didn't consider it a "socioeconomic" factor quite like poverty, age, or median income, so I left it out of the model. This meant that "education" was the only socioeconomic variable to benefit from population's influence, because its calculation had included it. In contrast, there's no "impoverished persons" statistic.

[Actually, I just generated that one, and a basic linear model shows that each "impoverished person" is expected to add $1.5 in library funding. Sweet! Condemn everyone to poverty and they will, uh, voluntarily pay more taxes to fund the library! Or maybe the town government will bleed hearts of gold! Yeah! Whatever we can dream up!]

So I think that's problematic. With that said, education is still an important socioeconomic predictor of library activity, just not nearly to the degree claimed.

That's not really the kind of analysis you should do, anyway. I've learned that causal inference is a bear, maybe even a monster. I now think it's pretty much impossible to disentangle these socioeconomic factors, so it doesn't make much sense to say things like "education is the real driver of library funding." They all reflect some underlying socioeconomic index.

Fixed for you.

How are you still reading this?

This paper I'm happy with but, due to academic norms, it's not as direct as it should be. I wanted to say this:

Some statisticians act like those undergrads who have memorized logical fallacies. If you tell someone they committed an ad hominem, then you win, right? And if you point out that someone violated a statistical assumption, then you also win. Best of all, you can go ahead and violate that assumption yourself and when called on it cite a study saying it's OK in your case. There's an SET denier who runs this game, loudly calling out other researchers for breaking the "rules" when he himself breaks them all of the time. Because that's how rules work. We have computers today, and in fact have had them for quite a while, so we don't have to cite random studies; we ourselves can simulate what happens given our data's structure when we violate assumptions.

But I couldn't say that, so the message comes off neutered and I'm not happy with how the materials are presented. Since completing that paper I've come to believe, fairly strongly, that methods in papers for most disciplines should be largely in an appendix. I dislike how bogged down the paper gets in the details.

I also dislike that I didn't describe the whole process. We had SET data, which as everyone knows is Likert and therefore ordinal. And as everyone also knows, there's no uncontroversial path forward. I had been reading about the power of simulating data, and I decided to just simulate and see what happens. I found that it didn't matter much. That's originally what I had planned to use until we reasoned out that humanities' readers would probably care more about real data than simulated data, so why didn't we marshal a bunch of real data instead?

Sure, and we went with that, but I missed an opportunity to explain that the simulations help you learn what kind of errors can occur when you have known parameters. I settled on referencing a study which did simulations, as that would probably be more credible than my own, and at the time I didn't really have the background knowledge to explain the above, at least responsibly.

Sidenote: When you teach yourself stuff, you have a random knowledge base, with awareness of fairly sophisticated methods but also possession of major foundational blindspots. Relatively early on I was simulating data (it's why I started using R) but if you had asked me to explain a link function I'd have channeled my school-aged self when called upon: stare confidently ahead, bluffing all the way.

I like that this paper is actually useful. It tackles a real problems—SETs for administrators who must use them—and offers a very simple heuristic that works as well as statistically "sound" methods. SET deniers like to declare, just get rid of SETs, don't use them at all, they're awful. Yet that's not only bizarre, the notion that we shouldn't be allowed to solicit student feedback, but also fanciful. Many administrators must use SETs in personnel decisions. And maybe SET deniers would tell them to just rate everyone great, because SETs are biased against disinterested teachers who hate their students, but anyone who wants to take their job seriously might want a more credible solution, and here we propose one.

When my university lost a big enough discrimination lawsuit to make headlines, the librarian in me had no choice but to read over 500 discrimination cases

I had been working on this paper, in some form, for the better part of six years, ever since my university lost a discrimination case. I find discrimination cases fascinating because they are pseudo-legal spaces where parties present cases to a hearing officer who ultimately determines which party was more credible, aka telling the truth. Early on, I spent a lot of time reading and annotating discrimination cases, swimming in the literature, and then I moved onto drafting something and finally thinking, hey, I might have an actual paper here.

I'm a bit remorseful that I didn't place it in an OA journal, but it was out of my discipline so I couldn't be super picky. It's a decent logistic regression, pretty basic, but it's not a complex analysis. Really I just try to examine what factors might influence winning/losing at a hearing. One referee thought it was pointless and no one would care about it, because only schmucks took obvious losers to public hearings, and he couldn't have been altogether correct since I have gotten several requests from law firms requesting full-text access. But I did agree with the point, and in fact my submission included that as a "limitation" (maybe I'll write more about limitations someday, and why they're nuts).

This is a sabermetric-like paper, where I combed a bunch of data and reported on what I had found, with no preconceived ideas. I didn't hypothesize that appeals would overwhelmingly lose; I just reported it. Ditto for the paper's odds ratios. Academics don't really do that. They prefer to focus on one thread, ideally one that's tied to some theory. Nevertheless, this paper unfortunately has much Frankenstein writing. What I mean by that is I could never quite discard my early thoughts, which acted like an anchor, confusing the whole paper.

Originally, the paper discussed disability discrimination, and how good of an idea it was to engage in an interactive process. The IP is not legally required, but it's worth doing, and hence if a hearing officer thinks you haven't engaged in one then you're all but doomed—it's how you run into ridiculous odds ratios like this paper has, where the odds of losing are like 91 times higher if you didn't engage in the IP (I groan at this statistic, given Gelman's example that smoking is associated with an OR of 5 for lung cancer, if I'm remembering correctly, and that you probably don't have ORs higher than that, and if you do then something's off, maybe not wrong, but off).

But the more cases I read, the more I found interesting issues of sexual and pregnancy discrimination. I think the paper would've been better served scrapping the disability stuff altogether and only focusing on sexual/pregnancy discrimination as well as retaliation. I didn't find much difference between private and public-sector employers when accounting for firm size. Large private-sector employers did about as well in hearings as the public-sector. The difference was driven largely by smaller employers with pregnancy and sexual harassment claims, and basically by definition there are no small public-sector employers. I believe it's probably because the obvious losers at larger firms don't make it to the hearing stage due to settlements, and the obvious losers at smaller firms go forward because the owners are insane and belligerent and/or because they don't/can't want to settle.

These cases drove home how awful workplaces can be. We like to mock the tiresome HR rules endemic in larger workplaces, the tedious trainings and whatnot. But I doubt you have a lot of managers in those places stapling bonus checks to condoms or asking employees to meet up in the conference room for a quick porn watch and follow-up Q+A.

the "use OLS for everything" vs. "don't" debate is neat because it really highlights how doing statistics well is much less about being right about anything than it is about making your wrongness as harmless as possible--Nick Huntington-Klein

Where I am now makes it harder to place papers. I only publish in open access journals that allow the release of all data. I now hate IMRD. In library science, very few journals for public libraries fit this mold. Not sure what education will look like. So I've got work sitting in the 'ole file drawer that I might just upload to ScienceOpen eventually.

I've learned a lot and am still largely clueless. Analysis is a talent, and, given that, you have very talented people...and not so talented people, which we should acknowledge. Not all research is created equally; some's good, some's excellent, and a lot is bad or run of the mill mediocre. It's what we'd expect from any distribution of something which involves skill.

There's technical skill, like knowing how to build an appropriate model, knowing how to code well in R; statistical domain knowledge, like understanding what correction to apply in such and such circumstance; artistic skill, what sports commentators might label inspiration or creativity, where you reason through hard problems; and subject matter expertise, understanding the field you're analyzing so you don't commit obvious blunders like omitting important variables, misclassifying relationships, stuff like that.

The experience has certainly been humbling. There's always someone who knows more than I do, and by more I mean way more, and by someone I mean virtually everyone. That's the nature of our modern world that's both too big and too small.

Once upon a time I used to work in a writing center, where you wouldn't be wrong to believe that one of my official duties involved Minesweeper. I was pretty good, averaging 110 seconds to clear expert. Then one day the stars aligned and I scored 81.

Welp, I smugly thought, that's it. Let's find a website to submit the new world record.

I had to have the world record. Like, I played this game almost every day, for a lot of hours, and it sure seemed like I went phenomenally fast. How could you do better? I wondered if the Minesweeper community awarded cash prizes.

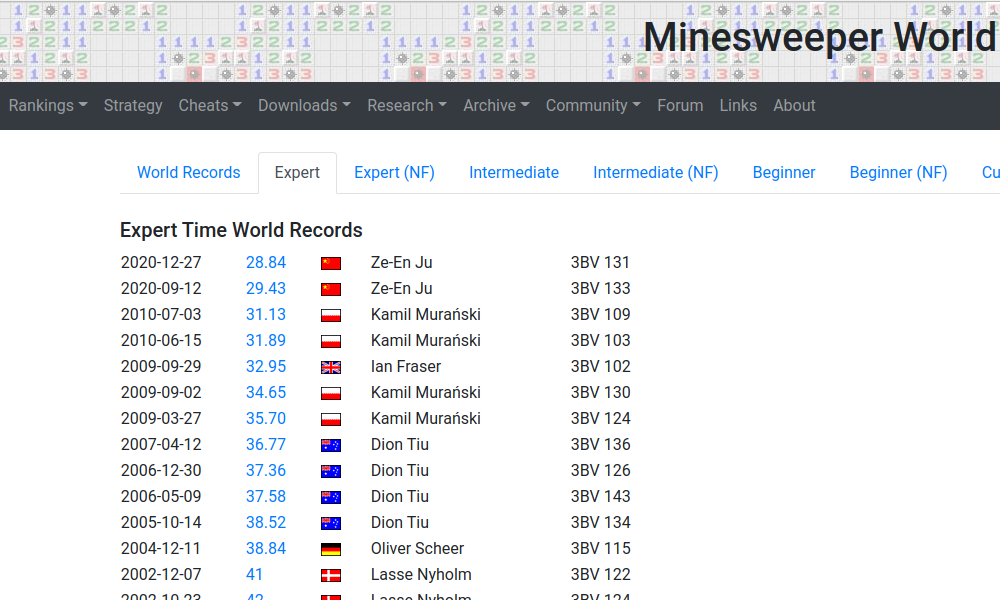
Yea so about that Dunning-Kruger effect.

Then I saw how wrong I was. Not only was 81 not a world record, it was nowhere close. "Sub-60" was a thing, as was "Sub-50"; these terms referred to expert clears below 60 and 50 seconds. The world record at the time was somewhere in the 30s (nowadays it's sub-30), less than half my score.

Pause. If we were all suddenly somebody else.

IMO, the best "stats work" is not in your textbooks or from your instructor (probably, anyway). Yes, those will give you firm foundations. But the best stuff comes from those doing the cutting-edge work. These folks will, above all, respect uncertainty and the havoc it can unleash on research. Where are they? Of course you'll find them in peer-reviewed journals, but you'll also find them engaging with their audiences on social media and their own blogs. That's kind of a tell that you've found someone whose work is high-quality; they're out there, with the people, unafraid to learn and confident to question themselves.

Here are some of the resources I recommend.

Josh Starmer's StatQuest. There's no contest here for comprehensive beginner's (and higher) material. This guy does an outstanding job explaining basically everything in a way that's not "dumbed down."

The Analysis Factor. Easy to read articles that highlight main statistical concepts. Useful when you're starting out and puzzled by some of the many confusing aspects of statistics. And if you want a clue as to how confusing it can get, go back and reread that paragraph I wrote about error = RMSE = Standard Error of the Estimate and whatever else. It helps to know the math, because then you don't get bogged down by the terms (you read the formulas to know what's happening), but you will often see just language.

Richard McElreath's lectures, especially those in his Statistical Rethinking series. IMO, this is the top resource in my list. You essentially audit a course taught by a legendary analyst. It's analogous to watching Magnus Carlsen stream chess. Ok, that's not quite right, because that would be more like listening to McElreath work through his own projects, but it's close enough.

Andrew Gelman's blog. You probably won't learn much here at first, because it gets fairly high level, but you'll see how a superb statistical mind (and his colleagues) reasons and approaches problems, in various contexts.

Chelsea Parlett-Pellereti's a veritable resource; she wrote the Crash Course statistics videos, which I've used; one thing about informal education is that you often have a lot of gaps, and you don't realize it until coming upon them, and thus you really always need primers. You can be merrily and confidently explaining Berkson's Paradox and then be caught completely off guard by a basic and common question like, "what do I do if my outcome variable's not normally distributed?"

Andrew Gelman and Jennifer Hill's multilevel modeling book. This was my go-to book for, like, everything. Not only are the MLM explanations good, but there's an entire course on regression here for you.

Daniela Witten's work, especially on machine learning and ultra especially Introduction to Statistical Learning. This book's amazing.

Andrew Ng's lectures on machine learning. A bit math-heavy but that's OK, because you should probably come here when you understand the basics of ML and are tired of not knowing the ghosts in those machines. Eventually you get to a point where you want to understand what makes these ML algos tick.

Daniel Lakens's blog. Really good reading that gets you thinking about the philosophy of statistics. For example, you might learn in class that you shouldn't use one-sided t tests, but Lakens argues convincingly that it's perfectly OK to use them. He also gives you a strong framework for hypothesis testing, if that's your thing; use equivalence tests.

Ulrich Schimmack's blog on replication. You can't unsee the replication crisis. You'll never look at a study the same way, that is, you'll be a total nihilist and not believe in anything anymore.

In my experience there aren't many good "books" on learning statistics. The ones I read when starting out I wouldn't recommend; I had just gotten them from a university library. There is, though, basically anything by Danielle Navarro, such as this applied one or this amazing one. Navarro's an absolutely brilliant thinker and engaging writer. Highly highly recommend.

Then there's McElreath's classic. And this one by Will Kurt seemed quite robust to my prior distribution of mass ignorance and my continual violations of bad habits and misinterpretation.